Month: May 2015

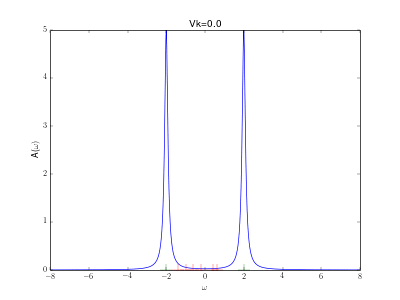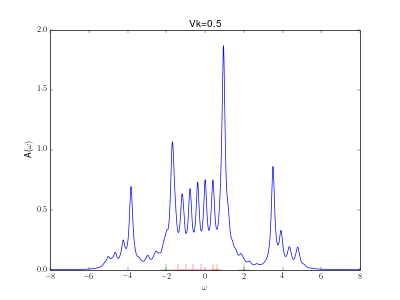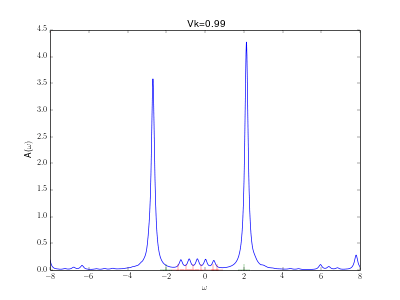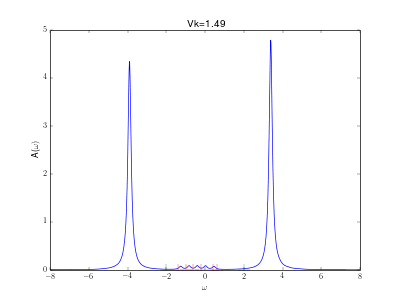
This animation shows the evolution for a simple Anderson impurity model (AIM) for rising hybridization strength from the atomic limit to a strongly coupled system.
The Hamiltonian reads with bath energies marked in red in the graph (implicit spin summation).

The excitation energies of the atomic limit at and are marked in green. A nice evolution from the atomic spectrum at small hybridizations with lower and upper Hubbard peaks over some kind of a Kondo resonance at the Fermi energy for intermediate hybridizations () to a fully coupled system with two peaks corresponding to the bonding and anti bonding orbital, one wandering down and one up in energy with increasing hybridization.